Введение
Статью на тему защиты хотелось
написать уже давно. Стремление это подкреплялось ещё и тем, что эта тема
начинает набирать популярность (уже две статьи, затрагивающие данную тематику,
представлены для конкурса). Действительно, в современном мире термин
“безопасность” приобретает всё более весомую значимость. Но он идёт вкупе с
такими вещами как криптография, значение которой столь же немаловажно. Пугает
то, что многие люди даже не догадываются, что это означает. Как ни прискорбно, но
среди них зачастую попадаются студенты технических факультетов крупнейших
университетов. А ведь именно они – оплот компьютерного мира завтрашнего дня. А
компьютерные технологии сегодня могут менять мировоззрения всего общества!
Ну, ладно я уже немного отвлекаюсь…
Как Вы уже поняли, речь в данной
статье пойдёт о криптографии – науке уже немолодой (краткая история её развития
от папируса до компьютера прекрасно изложена в книге Владимира Жельника) и перспективной.
Так же будут затронуты несколько немаловажных аспектов безопасности программ,
электронной почты и нашей жизни. Апофеозом статьи пусть будет реализация
программы с защищённой защитой.
Общие замечания и определения
Криптограф (криптоаналитик) – человек, занимающийся изучением,
разработкой, созданием и анализом криптографических методов; анализом стойкости
ключей, шифров; взломом шифров.
Исходное сообщение (открытый текст, сообщение, послание и
т.п.) – чистый
текст, который несёт некий логический смысл. Это может быть последовательность
байт, надписи, слова, звуки, файлы и т.п.
Взломщик – человек или машина, ведущая взлом шифра каким-либо
методом (прямым перебором или анализом свойств). Имеется в виду, что ключ
неизвестен. Либо некто, знающий ключ и ведущий взлом для выяснения надёжности и
стойкости шифра к атаке. Атака на шифр – анализ шифра и всевозможные
попытки получить исходное сообщение.
Шифр – зашифрованное сообщение.
SNBEM-версия ключа (или чего-то ещё) – это означает, что ключ (или
что-то ещё) зашифрован методом SNBEM,
и мы говорим о результате этого действия.
Ключ – просто пароль. Он участвует в шифровке/дешифровке. Обычно его знает
лишь один человек и бережёт как зеницу ока. Знание ключа – 100% разрушение
стойкости шифра.
Цикличный ключ – ключ, который при недостаточной длине образуется
дописыванием себя к своему концу. 2 3 -> 2 3 2 3
Шифрование – получение шифра из сообщения каким-либо
преобразованием. Обычно при участии ключа.
Дешифровка (расшифровка) – обратное действие шифрованию.
Простое число – целое число P, превосходящее единицу и имеющее только два делителя: 1 и P. 2, 3, 5, 7 – простые числа. 6 –
число не простое (составное), так как имеет в делителях так же 2 и 3. 6=1*2*3.
Простое число невозможно представить через подобное произведение. Существует
огромное количество методов проверки простоты числа. О них подробней можно
прочитать здесь.
Я же предложу самый простой метод – решето Эратосфена (правда, чуть-чуть
модифицированное):
Public Function
IsPrime(ByVal P As Long) As Boolean
Dim Max As
Long, F As Long
IsPrime =
False
If P < 2
Then Exit Function
If ((P And
1) = 0) Then
IsPrime
= (P = 2)
Exit
Function
End If
If ((P Mod
3) = 0) Then
IsPrime
= (P = 3)
Exit
Function
End If
Max =
CLng(Int(Sqr(P)))
For F = 5
To Max Step 6
If (((P
Mod F) = 0) Or ((P Mod (F + 2)) = 0)) Then Exit Function
Next
IsPrime = True
End Function
Аддитивная разбросанность - это показатель рассеивания (т.е.
неопределённости ~ энтропии Шеннона) зашифрованного сообщения. Мультипликативная
разбросанность аналогична, но имеет большую степень рассеивания. И вправду,
сложение намного меньше увеличивает число, нежели умножение. Покажем суть на примере:
Сообщение:
0 2 2 1 1 2 2 3 1 2 3
Ключ: 6 3
7 2 3
При аддитивной разбросанности (складываем элемент
сообщения с элементом ключа. По необходимости ключ циклично повторяем): 6 5 9 3
4 8 5 10 3 5 9
При
мультипликативной (умножаем): 0 6 14 2 3 12 6 21 2 6 18
Получаем, что для аддитивной разбросанности диапазон равен
[3..10] (в идеале - [0..10]), а для мультипликативной: [0..21]. Эти диапазоны
показывают, в каких рамках нужно искать символы при взломе шифра. Согласитесь,
что при мультипликативности существует в 2,1 раза больше вариантов!
Следовательно, и искать в такую же степень раз сложней. Сложная
разбросанность – это комбинации аддитивной и мультипликативной
разбросанностей.
723 – магическое число криптографии. Есть математические доказательства,
что для множества систем, которые могут оперировать лишь с целыми ключами из
диапазона [0..1000], ключ 723 по усреднённой статистике будет проверяться самым
последним.
Двусторонний метод шифрования (с обратным ходом) – метод, который содержит в себе
процедуры для шифрования и расшифровки. Т.е. если x – исходное сообщение, а Fkey(x) – зашифрованное, то двусторонний метод содержит
ещё функцию Gkey(), которая обладает свойством: Gkey(Fkey(x))=x
для любого значения x. Функция Fkey(x) шифрует сообщение x ключом key, а Gkey(x) соответственно расшифровывает.
Односторонний метод шифрования (без обратного хода) – метод, который может лишь
зашифровывать сообщение. Процедура расшифровки отсутствует. Такие методы
применяются в крупных учреждениях, таких как банки, правительственные структуры
и т.п. Сначала не всегда понятно, зачем собственно нужны и чем хороши такие
методы. Что ж поясню на конкретном примере:
Ситуация 1
Ситуация описывает банковскую систему, которая не
использует одностороннего шифрования данных клиента:
Есть банк.
Есть клиент банка,
т.е. человек, который хранит в нём деньги. Есть служащий банка, который
обслуживает клиента и, наконец, есть база данных с данными по каждому клиенту
(именно данные в этой базе не шифруются односторонним методом!).
Процесс получения денег клиентом выглядит
следующим образом: клиент сообщает служащему свой личный пароль. Служащий
просто сверяет его с паролем в базе данных и лишь в случае совпадения выдаёт
клиенту деньги. А теперь обратная сторона процесса: пусть служащий банка не
чист на руку и решил присвоить деньги клиента. Ничто не мешает ему взять из
базы данных требуемый пароль и произвести операции со счётом клиента. Когда
клиент начнёт вопить, что он не снимал деньги, кто ему поверит? Никто.
Служащему достаточно сказать, что клиент приходил, называл правильный пароль
(вот он у меня на листике записан!) и полностью обналичил счёт.
Ситуация 2
Ситуация описывает банковскую систему, которая использует
односторонний метод шифрования данных клиента:
Всё выглядит также, с одним лишь
отличием: пароль клиента хранится в базе данных в зашифрованном виде
(односторонним методом!).
Процесс получения денег клиентом
выглядит следующим образом: клиент сообщает служащему свой личный пароль.
Служащий шифрует полученный пароль односторонним методом, и результат сверяет с
паролем в базе данных и лишь в случае совпадения выдаёт клиенту деньги.
Теперь служащий может взять пароль клиента из
базы данных, но реального пароля (который должен сообщить клиент) он знать не
будет! Воровство не удастся.
Могу предположить, что кто-то из читателей
вскрикнет – надул ты нас, батенька! Во втором случае служащий может украсть
деньги! Ведь именно пароль из базы данных нужен для доступа к деньгам. Начхать
нам на реальный пароль клиента! И будет прав такой умный читатель! В банковской
системе реализация описанного процесса намного сложней и в ней участвуют ещё
такие персонажи, например, как снимок времени, ЭВМ и т.д. Пример просто
показывает суть системы.
Подумаёте логически, вы же когда сообщаете
пароль к своей электронной почте, например, через веб-форму, не знаете, что так
с ним происходит. Он может быть автоматически (на программном уровне)
сравнивается с паролем из базы данных, а может быть, его читает админ и даёт
добро или не добро на Ваш вход. В первом случае лишь машина знает секретные
данные, и их сохранность зависит лишь от программистов, которые разрабатывали
эту систему. Во втором случае всё зависит от корысти админа. Мы опять же не
можем иметь стопроцентную уверенность в сохранности наших личных данных. И
всё-таки миллионы людей ежедневно отдают свои пароли на съедение веб-формам!
В банке служащий тоже может быть человеком или
ЭВМ. Таким образом, сохранность наших секретов ложится на плечи сумрачного НЕКТО,
который скрыт от нас пеленой тумана, но на чью порядочность, стабильность и
защиту мы искренне надеемся, молимся и верим. Именно поэтому надо параллельно
разработке защиты разрабатывать ещё защиту для защиты.
Я попытался объяснить этот сложный вопрос как
можно проще, но думаю, что у Вас всё равно есть некоторые сомнения, возможно.
Критика принимается! Очень приятно вести дискуссию с людьми, интересующимися криптографией.
А вот Вам ещё одна мысль: если юзер забыл пароль к своему e-мылу, он может получить его через
систему напоминания пароля, указав некоторые данные (девичью фамилию матери,
иною свою мыльницу и т.п.). Так, что же получается? Пароли хранятся в открытом
виде (ну, по крайней мере, не зашифрованы односторонне)? Остаётся лишь гадать,
что будет, если базу стянут…
SNBEM
SNBEM – Simple Numbers
Based Encryption Method (метод шифрования основанный на простых числах). Я
написал этот метод на ASP,
когда создавал сайт для Инвестиционного
Клуба, который требовал нетривиальной защиты паролей для клиентов. Система
аутентификации должна работать не с реальными паролями, а с их шифрами. И в
случае утери пароля, восстановить его будет невозможно – нужно создавать другой
пароль.
Требуемая защита должна была
соответствовать двум требованиям:
1. Метод должен быть односторонним
2. Быть стойким к взлому
И вот что вышло:
1 Function
SNBEM(Text)
2 Dim
I,J,K,L,P,R,T
3 T=Text
4 For
P=1 To 2
5 R=""
6 L=Len(Text)
7 For
I=1 To L
8 J=(L*I+723)
Mod (L+I)
9 For
K=I To Len(Text)
10 J=((J*Asc(Mid(Text,K,1)))
Mod 256)
11 Do
While Not isPrime(J)
12 J=J+1
13 Loop
14 Next
15 J=J
Mod 256
16 R=Chr(J)
& R
17 Next
18 Text=R
19 Next
20 Text=T
21 SNBEM=R
22 End function
Комментарии к коду: шифруем сообщение Text (1). Оно передаётся в переменную T (3). Сообщение шифруется 2 раза –
слева направо и справа налево. Это даст большую устойчивость к взлому (4
строка). В R будут хранится уже зашифрованные
символы сообщения (5). Делаем сложную разбросанность, привлекая магическое
число криптографии 723 (8 строка). В девятой строке мы усиливаем зависимость
текущего шифруемого символа от последующих в сообщении. Применяем
мультипликативную разбросанность (10). В цикле Do…Loop
как раз создаётся односторонность метода (11-14)! Выравниваем значение текущего
шифруемого символа (15) и дописываем к началу выходного сообщения (16). Теперь
отправляемся на второй круг (19). Всё (20-22)!
Роман Ройтер в своей статье говорил
о том, что в программе лучше не хранить пароль. Я согласен. Но можно хранить
его SNBEM-версию! Т.е. вместо кода:
Key=inputbox(“Ваш пароль:”)
If key=”qwerty”
then msgbox “Cool!” else msgbox “Bad key”
пишем
Key=snbem(inputbox(“Ваш пароль:”))
If key=”£Gé[1]/”
then msgbox “Cool!” else msgbox “Bad key”
SNBEM превратит qwerty в £Gé[1]/. Это и пишем в проверке (лучше проверять не
целиком, а побайтно). Реального пароля нет! Остаётся опасаться только перехвата
проверки. Но об этом позже.
Одноразовый блокнот
Данный метод в
совершенстве использует алчное стремление многих людей знать всё.
Он действительно даёт
человеку такую возможность!
По заявлению Брюса Шнейдера (всемирно
известного криптолога и гуру), этот метод является идеальным (т.е. 100% стойким
к взлому) и я разделяю его точку зрения. Каких бы сложностей ни воротили
крупнейшие компании мира в разработке новых сверхстойких алгоритмов шифрования
(MARS IBM’а чего только стоит),
одноразовый блокнот умиляет своей простотой (всё гениальное – просто!) и
лёгкостью исполнения. Обычного человека этот метод только рассмешит своим
наполеонизмом (куда ж такой крохе тягаться лезть к DES!!! Слон и Моська одним
словом) и банальной схожестью с шифрами простой замены. А вот криптоаналитик с
мировым именем проснётся ночью в холодном поту, не приведи господи ему увидеть
очертания этого бронированного чудовища во сне!
Так чёго же побоится
криптоаналитик, если случится ему расшифровывать шифр полученный одноразовым
блокнотом? Простой пример. Возьмём лишь только могучий наш русский язык. Пусть
взломщик перехватил 5-ти символьное зашифрованное сообщение и знает, что оно
зашифровано одноразовым блокнотом и что это одно из слов русского языка. Начнём
с того, с какой вероятностью он узнает истинное сообщение: я не знаю, сколько в
русском языке 5-ти символьных слов, поэтому будем ограничиваться потолком.
Всего в русском существует 39135393 различных 5-ти символьных сообщений (33^5).
Значит, вероятность найти единственно верное – не меньше 1/39135393. Не так уж
и плохо, скажет взломщик! А теперь раскроем один секрет нашему криптоаналитику:
перехваченный им шифр со 100% вероятностью может быть любым из 39135393 русских
пятибуквенных сообщений! Ну-ка, выбери правильное! Любое из пятибуквенных слов
русского языка может быть получено в результате взлома!!! Народ ликует… занавес…
Только знание правильного ключа даёт правильное сообщение. Так в чём же секрет
метода. Да нет секрета!!! Вот он метод (приведено шифрование, для дешифровки
нужно чуть-чуть подправить 7-ую строку):
Private
Function OnceTimeNotepad(byval Text as string,byval Password as string) as
string
Dim
Res as string, I as long
Do
while len(password)<len(text)
Password=password & password ‘ создаём цикличный ключ
Loop
For
i=1 to len(text)
Res=Res & chr(clng(asc(mid$(text,I,1)))+clng(asc(mid$(password,I,1)))
mod 256)
next
oncetimenotepad=res
End function
10 строк ужаса,
набранных мною по памяти на клавиатуре за 1 минуту 30 секунд! Теперь остаётся
лишь совместить SNBEM и одноразовый блокнот, и криптоаналитики могут спокойно
отправляться на пенсию!
Почёму одноразовый?
Важная особенность метода: в качестве пароля нужно брать случайный набор
символов. Но никогда не используйте его повторно! Если криптоаналитик
перехватит от Вас 2 разных сообщения, зашифрованные одним и тем же ключом, то
простой анализ статистических свойств двух шифров обрушит всю грандиозную
стойкость метода!!!
Генерация ключей и случайных
последовательностей
Ясно, что ключ оказывает большое влияние на стойкость
системы шифрования. Чем сложнее будет ключ, тем труднее взломщику подобрать его.
Существуют огромные чёрные списки ключей, которые не рекомендуется
использовать. Они дают понять, что в качестве ключа лучше не использовать
последовательности символов, которые несут какой-либо логический смысл. Вот,
например, плохой вариант ключа: alexsandrthatlivesinnovosibirsk. Хороший ключ: StU5_Nist67. Хотя он намного короче первого ключа, подобрать
его для взломщика намного сложней.
Как получать стойкие ключи? Хороший вариант –
генерировать его случайным образом. Только надо обратить внимание на эту самую
случайность. Код
Randomize timer
Key=int(rnd(1)*123456789)
не даёт случайного номера! Есть зависимость от timer’а, а любая зависимость в случайной
последовательности – очень плохая вещь. Выход один: использовать специальные
алгоритмы генерации случайных последовательностей (о них великолепно написано в
книге ‘Криптография от
папируса до компьютера’), либо использовать общеизвестные случайные
величины (некоторые их части). Рассмотрим второй случай:
К общеизвестным случайным величинам относятся
такие константы, как “Пи”=3.14… и “e”=2.58… У числа ∏ известны более 2 миллиардов знаков после
запятой и учёные не обнаружили среди них никаких закономерностей. Поэтому можно
использовать любую часть этого числа в качестве случайной последовательности.
Возьмём 125 цифр начиная с миллионного разряда после запятой в записи числа
∏ и мы получим случайное 1000 битное число. Запись числа ∏ (её
можно найти на математических сайтах) влезет на один компакт диск. Достаточно
создать функцию для получения последовательности нужной длины:
Public Function
GetRandomFromPi(ByVal Start As Long, ByVal Length As Long) As String
Dim FF As
Integer, Ret As String
Ret =
String$(Length, " ")
FF =
FreeFile
Open
"d:\pi.dat" For Binary As #FF
Get
#FF, Start, Ret
Close #1
GetRandomFromPi
= Ret
End Function
Секреты внутренностей Вашей
программы
Поставим перед собой цель написать программу, которая будет работать
лишь при правильно введённом пароле при запуске. Написать защитный механизм
можно различными способами, но всегда будет возникать ряд проблем с реализацией
“защиты” нашей защиты. Итак, всё по порядку: создадим самую простую программу
на VB 6.0:
Option Explicit
Sub Main()
End Sub
Она состоит из одного модуля, все
формы удалены. Откомпилируем в c:\vb\crypt.exe.
В любом HEX-редакторе просмотрим содержимое
полученного файла (я использую HEX Workshop 3.01, но подойдёт простой DN или FAR – дело вкуса):

Из статистики видно, что 3516 байт из
16384’x являются пустыми. Их изменение не
повлияет на работоспособность всего exe-файла. Т.е. диапазон байт [582..4090] может использоваться для наших
нужд (но необходимо следить за этим диапазоном, так как его границы могут
варьироваться!). Сюда можно записать ключ для шифрования, расшифровки, а лучше
его SNBEM-версию! Итого мы получим 3516 байт
* 8=28128 битовый ключ! Таким образом, он не будет явно присутствовать в коде
и, следовательно, не будет занимать дополнительное место. Доступ к шифрованному
ключу можно получить, побайтно считав его из exe-файла:
Dim FF As
Integer, Key As String
Key =
String$(5, " ") ‘ 5 – это длина пароля
FF = FreeFile
Open
"c:\vb\crypt.exe" For Binary As #FF
Get #FF, 582,
Key
Close #FF
Выберем для нашей программы пароль.
Пусть будет Yxine, хотя лучше брать что-то длинней.
Об этом я уже писал. Вычисляем SNBEM
для Yxine: побайтно это выглядит так: 41 157
79 101 149. Переводим в HEX:
29 9D 4F 65 95 и записываем в exe-файл, начиная с 582 байта (для этого дела лучше
написать небольшую программку, так как после каждого компилирования ключ будет
пропадать):
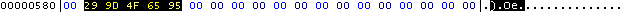
Всё, ключ вшит, хотя реального
пароля в программе нет! Считывать его мы уже научились. Остаётся самое слабое
звено: проверка пароля.
Хакер может изучить, как работает алгоритм
шифрования и вся наша защита. Он может спокойно вычислить место, где мы храним
наш шифрованный ключ. Пожалуйста! Хакер может вырвать кусок защиты (функции isPrime и SNBEM). Но так как SNEM не имеет способа к дешифровке, то эта лазейка для
поиска ключа даст взломщику лишь возможность для тупого перебора все вариантов.
Т.е. теперь хакер знает SNBEM
нашего пароля и знает, как шифруется открытый ключ. Длина нашего пароля 5
символов. Получаем, что хакеру нужно перебрать 256^5 ключей (т.е.
1.099.511.627.776 вариантов). А если бы мы использовали все 3516 байт для
ключа: 256^3516 вариантов!!! Перебор явно отпадает. Хакеру остаётся либо найти
точку сравнения паролей и поменять условный переход на безусловный (очень
простой вариант), либо полностью ликвидировать защитный алгоритм из кода
программы (очень сложный вариант даже для бывалого хакера). Не будем
рассматривать второй путь, ограничимся только первым. Дописываем в Main строку:
UserKey = InputBox("Введите пароль:")
SNBEM от UserKey пока не берём. Сверять Key и UserKey напрямую или какими-то
модификациями строк не советую – это очень легко перехватить. Хорошим способом
сверки паролей в данном случае является закрытый код. Т.е. алгоритм проверки
правильности пароля должен быть зашифрован (OneTimeNotepad c нашим ключом в качестве пароля –
отличный вариант). Шифр кода проверки можно записать в exe-файл после нашего SNBEM ключа, т.е. начиная с 587-ого байта.
Проверка правильности ключей должна
быть вшита в этот алгоритм. Пример реализации интерпретации можно найти в исходниках
RIPL. Сам алгоритм может выглядеть, например, так (я
взял язык RIPL, хотя можете придумать что-нибудь своё
J):
Program Check
Memory
String
Key1,Key2,Bool
End Memory
Proc Main
Copy Key1,DirectDim(Key)
Copy Key2,DirectDim(UserKey)
Copy Bool,key1=Key2
If bool->endp
DirectCall Done
Endp:
End Proc
End Program
Функция DirectDIM() вытаскивает значение переменной
из VB-программы и передаёт его в RIPL-программу. DirectCall вызывает выполнение VB-процедуры в случае правильности
пароля.
Таким образом, проверка пароля происходит
косвенно в зашифрованном фрагменте алгоритма. Получить к ней (проверке) доступ
или перехватить её означает взломать шифровку одноразовым блокнотом или
перелопатить весь exe-файл на
уровне ассемблера, на что, согласитесь, пойдёт не каждый даже умелый хакер. Для
запудривания мозгов взломщика можно добавить в этот алгоритм какой-нибудь мусор
и пустые проверки.
Доведём дело до конца:
Шифруем данный кусок программы
одноразовым блокнотом, представляем всё это дело в байтах и переводим в
16-ричную систему счисления. Записываем всё это в наш exe-файл начиная с 587-го байта. Фрагмент теперь выглядит
так:

Защита готова! В программе нет
нашего реального пароля (Yxine),
есть только его SNBEM-версия,
плюс при этом сам алгоритм проверки подлинности пароля зашифрован с помощью
этого же пароля! Защита защиты в чистом виде! Полный код программы выглядит так:
Option explicit
Sub Main
Dim FF As
Integer, Key As String, UserKey as string, Code as string
Key =
String$(5, " ")
FF = FreeFile
Open
"c:\vb\crypt.exe" For Binary As #FF
Get #FF, 582,
Key
Close #FF
Userkey=inputbox(“Введите пароль:”)
Code=String$(200,”
“) ‘
длина зашифрованного кода
FF = FreeFile
Open
"c:\vb\crypt.exe" For Binary As #FF
Get #FF, 587,
Code
Close #FF
‘ теперь осталось только интерпретировать
программу, записанную в переменной Code. См. RIPL
End Sub
Sub Done()
Msgbox “Пароль введён
правильно!”
End Sub
Всего доброго!
yxine@mail.ru
http://www.yxine.km.ru