Несколько слов от автора или ‘А чё ваще?’
Всё началось банально: я купил
журнал ‘Компьютерра’. Среди множества интересных новостей, мне попалась одна
очень любопытная: найдено 39-тое число Мерсенна. Оказалось, что это любопытное
число представляется в виде 2p-1 и что существует проект распределённых вычислений (http://www.mersenne.org),
дающий возможность всем искать такие полезные числа.
Собственно, зачем это надо, спросите Вы. Ну,
во-первых, деньги! Тот, кто найдёт новое число, получит неплохих бобов.
Во-вторых, счастливчик попадёт не только в книгу рекордов Гиннеса, но и
навсегда оставит своё имя в анналах истории математики. Что ж, вполне
заманчиво, и если вы математик-энтузиаст, то это вдвойне заманчиво.
Проект (далее GIMPS) предоставляет Вам программу для произведения
тестирования и числа, которые нужно тестировать. Это также неплохой способ
избежать холостой работы процессора Вашего компьютера. Да и программа требует не
так уж много памяти и совершенно не влияет на работу приложений или чего бы там
ни было.
Итак, я вступил в ряды GIMPS. Через некоторое время захотелось
иметь у себя на компьютере статистику по результатам работы проекта (не
хотелось убивать время на тестирование чисел, которые уже проверены). С сервера
её можно было скачать только в текстовом виде, и к тому же она была не очень
полной. Программа была написана
быстро. Она выводила всю нужную статистику. Но захотелось, чтобы она могла
самостоятельно тестировать Мерсенновских кандидатов. Благо в документации к
программе все методы были хорошо описаны. Были даже исходники всей программы на С++ вперемешку с Assembler’ом… А надо на Visual Basic’е. Выход нашёлся быстро – написать
всё своими ручками. Вот тут-то и начались проблемы. Алгоритмы-то написать было
очень просто. А вот как работать с числами, которые не умещаются ни в каких
числовых типах, начиная от byte и
заканчивая Double? Значение числа 2p-1 растёт очень быстро, и уже при p=100 алгоритмы перестают работать
из-за переполнения, а как быть с p=21.114.997,
например?
Вот тут и приходит на ум использовать
длинную арифметику (далее ДА), благо в VB есть такой замечательный тип как String!
После длительных поисков в Internet’е мной были найдены несколько
примеров реализации алгоритмов ДА. С ними можно ознакомиться здесь:
http://algolist-demo.makecd.ru/maths/longnum.html
Материала в сети по этой теме подозрительно мало, да и написано
всё на C/Assembler/Pascal. Многие алгоритмы были слишком
медленными или с большими ограничениями, да и переписывать с С на Visual Basic не очень хотелось. И опять пришлось
всё делать своими мозгами и руками. В итоге получился хороший набор функций,
который более-менее быстро работает1 и не сложен в освоении. Все функции
реализованы только для положительных целых чисел (из-за специфики
разрабатываемой мною программы, где этого было вполне достаточно), но
переписать всё для отрицательных и дробных проще простого если принять тот
факт, что число 1234.3456, например, представляется двумя целыми, разделёнными
точкой, а знак “-” меняет операцию сложения на вычитание и наоборот. Пусть
такая ‘расширенная’ реализация будет вашим домашним заданием.
1 Первоначальная
реализация работала на несколько порядков хуже, чем предложенная сейчас. Я
уверен, что вполне можно написать ещё более быстрые алгоритмы, но я пока
исчерпал свой потенциал. Что касается алгоритмов, используемых в GIMPS: там всё
основывается на быстром преобразовании Фурье. Его сложно реализовать, но
скорость работы впечатляет.
Описание алгоритмов с примерами или ‘По следам Вирта’
Вводное
замечание: все числа будут храниться в переменных типа String, если не указан другой способ.
Итак,
нужны базовые операции математики:
1.
Сравнение чисел
2.
Сложение чисел
3.
Вычитание чисел
4.
Умножение чисел
5.
Деление чисел
6.
Возведение в
степень
7.
Взятие модуля
(остаток от деления)
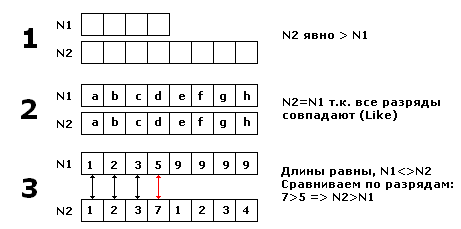
Сравнение:
N1, N2 – два числа.
1.
Если длины
чисел не равны, то больше то число, чья длина больше. Это элементарно.
2.
Остаётся
случай, когда длины чисел равны:
a.
N1=N2 (легко проверяется функцией Like)
b. Иначе: поочерёдно сравниваем
разряды обоих чисел начиная со старшего и двигаясь в направлении к младшему.
При первом же несоответствии разрядов, большим признаём то число, чей разряд
оказался большим.
Наглядно это выглядит так:
Сложение:
Вспомним школьную программу: самое простое – сложить два
числа столбиком. Реализуем немного усовершенствованный алгоритм такого сложения: (N1=953072, N2=061234)
1. Меньшее по длине число дополним
нулями слева (до длины большего по длине числа – возможно не очень хорошее
решение, зато не надо возиться с пересчётом адресов в массиве). Выпишем первое
число по разрядам:

2. К этому числу поразрядно прибавим
второе:
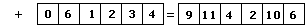
3. Нормализуем число поразрядно: будем
двигаться от младшего к старшему разряду. На каждом шаге: если текущий разряд
больше 9, то следующий разряд увеличиваем на 1, текущий уменьшаем на 10. Если в
конце в памяти останется 1, то значит, что в числе появился новый разряд, и мы
должны в начало результата дописать 1:
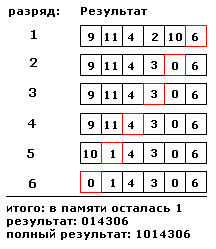
Этот метод хорошо реализуется с помощью байтового массива.
Размерность массива равна длине наибольшего из суммируемых чисел. Ещё одна
проблема, которую надо решить: преобразование массива в String. Как это реализовано смотрите в
исходнике (число 48).
Вычитание:
Алгоритм очень похож на суммирование. Но есть несколько
небольших отличий (N1=12345, N2=9374):
1. Меньшее по длине число дополним
нулями слева. Выпишем первое число по разрядам, прибавляя одновременно к
каждому разряду 10:
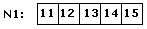
2. От этого числа поразрядно отнимем
второе:
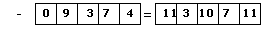
3. Нормализуем число поразрядно: будем
двигаться от младшего к старшему разряду. На каждом шаге: если текущий разряд
меньше 10, то следующий разряд уменьшаем на 1, иначе текущий разряд берём по
модулю 10:
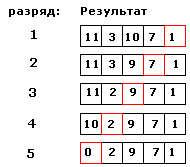
4. Теперь остаётся лишь убрать лишние
нули из левой части результата. Получаем число 2971.
При реализации следует помнить, что если N1=N2, то мы получим одни нули, и в пункте 4 нужно будет
оставить 1 ноль. Это и будет результатом.
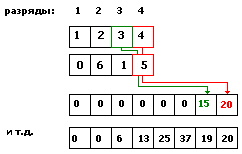
Умножение
Как будем
умножать? Ну, конечно в столбик, по школярски! (N1=1234, N2=615).
1.
Стандартно: дополним
меньшее по длине число нулями слева.
2. Возьмём 2*длина_числа нулевых
ячеек. Умножаем на 2 т.к. при умножении мы можем получить новые разряды в
количестве от 0 до длины наибольшего числа: 9*1=9 (нет новых разрядов) и 99*99=9801
(2 новых разряда).

3.
Двигаемся по
первому числу начиная с младшего разряда к старшему.
4.
Двигаемся по
второму числу начиная с младшего разряда к старшему
5.
Произведение
выбранных разрядов прибавляем к значению ячейки с адресом, равным сумме номеров
выбранных разрядов:
6.
Идём на шаг 4
7.
Идём на шаг 3
8.
Теперь
нормализуем результат. Как и в алгоритме сложения!
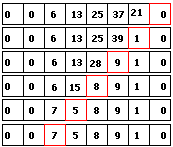
9.
Получаем
результат
758.910
P.S. при реализации следует помнить, что массив надо
брать из элементов типа Long.
После нормализации его нужно будет перевести в байтовый массив и конвертировать
последний в String.
Деление
При
делении нам надо найти целую часть и остаток. Остаток находится с помощью
взятия модуля - смотрите алгоритм ниже. Если в этом алгоритме каждый раз
подсчитывать количество нулей дописываемых ко второму числу и брать во внимание
число, на которое умножается массив, то тем самым легко получить целую часть.
Возведение в степень
A – основание (String), N – степень (Long). Вычислим AN
Для любого основания верно: A1=A и A0=1. Это
можно принять за точки выхода из рекурсии. Сама процедура возведения будет
рекурсивна с глубиной [log2N].
1.
Если N=0, то
результат 1
2.
Если N=1, то результат – само число A
3.
Делим N пополам и берём целую часть (*
если N нечётно, то обратите внимание на
шаг 6)
4.
Повторно
вызываем процедуру, только уже с новым N
5.
Результат
возводим в квадрат (умножаем сам на себя)
6.
Вспоминаем:
если N до вызова рекурсии было нечётным,
то результат умножаем на A
Пример:
211
N=11<>{0,1}
N=[N/2]=5
N=5<>{0,1}
N=[N/2]=2
N=2<>{0,1}
N=[N/2]=1
N=1=1 => Результат=A=2
Результат=Результат*Результат=2*2=4
N было равно 2 – чётное
Результат=Результат*Результат=4*4=16
N было равно 5 – нечётное =>
Результат=Результат*2=16*2=32
Результат=Результат*Результат=32*32=1024
N было равно 11 – нечётное =>
Результат=Результат*2=1024*2=2048
Итого: 211=2048.
Глубина рекурсии равна 3.
Наглядно:
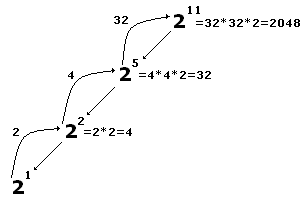
Взятие модуля
С этим алгоритмом пришлось изрядно повозиться из-за того,
что операция Mod практически нигде не описана. Опять
вспоминаем математику:
A
mod A=0
A
mod 1=0
A mod B=C означает,
что существует такое положительное целое число K, что B*K+C=A.
C нам надо найти. Что ж, существует
очень простой способ: отнимать от A число
B до тех пор, пока A>=B. В итоге получим C. Но представьте только, сколько операций вычитания
придётся сделать при больших числах!!! Надо как-то оптимизировать вычитание. До
сих пор мы не использовали число K.
Каким оно может быть? K может
быть разложено на произведение чисел. Чем оптимальнее будут выбраны эти числа,
тем лучше! Самое лучшее решение, что приходит в голову: выбирать K поразрядно (по степеням 10). Протестируем
идею - рассмотрим пару примеров:
1. 1234 mod 7=2
2. 1237 mod 70=44 44
mod 7=2
3.
1237 mod 700=534 534 mod 70=44 44 mod 7=2
Значит, мы
можем варьировать значением числа K~B (с определёнными условиями)!
Воплощаем
мысль в алгоритм:
1.
Откинем все
частные случаи и тогда получим, что: A>B
2.
Итак, если A>B:
3.
Будем умножать B на 10 до тех пор, пока длины чисел A и B не сравняются.
4.
Если A=B, то mod=0
5.
Если A<B, то получается, что мы переборщили с умножением ->
делим B на 10
6.
Поочерёдно
умножаем B на i=1,2,3,… пока B не станет больше A
7.
Берём
предыдущее число (i), на
которое было умножено B,
и выполняем A=A-B*i
8.
Идём на шаг 2
9.
Результат=A
Возможно,
пример поможет понять алгоритм:
356395
mod 37=C, C=?
A=356395
B=37
A>B – верно
Умножаем B на 10, пока длины не сравняются: B=370000
B>A – с нулями мы переборщили => B=37000 ** умножили на
1000
B*1=37000
B*2=74000
B*3=111000
B*4=148000
B*5=185000
B*6=222000
B*7=259000
B*8=296000
B*9=333000
B*10=37000
B>A – верно
A=A-B*9=356395-333000=23395 **
умножили на 9
A=23395
B=37
A>B
– верно
B=37000 – перебор => B=3700 **
умножили на 100
B*1=3700
B*2=7400
B*3=11100
B*4=14800
B*5=18500
B*6=22200
B*7=25900
B>A – верно
A=A-B*6=23395-22200=1195 **
умножили на 6
A=1195
B=37
A>B
– верно
B=3700 – перебор => B=370 **
умножили на 10
B*1=370
B*2=740
B*3=1110
B*4=1480
B>A – верно
A=A-B*3=1195-1110=85 **
умножили на 3
A=85
B=37
B=370 – перебор, B=37 **
умножили на 1
B*1=37
B*2=74
B*3=111
B>A – верно
A=A-B*2=85-74=11 **
умножили на 2
A=11
B=70
A<B
=> C=11
Всего
потребовалось: 4 вычитания и 19 сложений (куда пропали умножения, смотрите в
исходном коде)
А если бы мы пользовались простыми вычитаниями, то их
потребовалось бы: 9632 штуки!!! Кстати, это и есть число K – целая часть от деления A на B, а ведь из приведённого примера мы можем вычленить
это число, если обратим внимание на строки, помеченные **: если выпишем
вынесенные числа, то получим: 1000 9 100 6 10 3 1 2. А теперь расставим арифметические знаки:
1000*9+100*6+10*3+1*2=9632. Это свойство используется в алгоритме деления!!!
Исходные коды с комментариями автора или ‘Вот оно как!’
Option Explicit
С начала несколько вспомогательных и просто полезных функций:
Public Function DigitPoints(ByVal Number As String) As String
‘ Эта функция отделяет каждые 3 разряда числа точкой. Ведь 14.879.204.579.493.534 выглядит намного лучше, чем 14879204579493534.
‘ Возможно, это не самая оптимальная и быстрая реализация, но хотя бы работает.
Dim Num As String, I As Long, J As Long, Ret As String
J = 0
Ret = ""
For I = Len(Number) To 1 Step -1
J = J + 1
If J Mod 3 = 0 Then Ret = "." & Mid$(Number, I, 3) & Ret ‘ каждый третий разряд!
Next
‘ не будет ли наше число начинаться с точки? (в случае, когда длина числа кратна 3 – будет!) -> Если да, убираем первый символ.
If Len(Number) Mod 3 <> 0 Then Ret = Left$(Number, Len(Number) Mod 3) & Ret Else Ret = Right$(Ret, Len(Ret) - 1)
DigitPoints = Ret
End Function
Public Function ResetZero(ByVal N1 As String) As String
‘ просто убираем лишние нули из начала строки (числа): 0004562 -> 4562
On Error Resume Next
Dim I As Long, Tmp As String
For I = 1 To Len(N1)
If Mid$(N1, I, 1) <> "0" Then Exit For ‘ передвигаем указатель i по числу, пока на встретим не 0
Next
Tmp = Right$(N1, Len(N1) - I + 1) ‘ Вырезаем ненужный мусор
‘ Если строка состояла из одних нулей, то оставим один нолик на память!
If Tmp = "" Then ResetZero = "0" Else ResetZero = Tmp
End Function
‘ Сравним два числа:
Public Function isEqual(ByVal N1 As String, ByVal N2 As String) As Boolean
On Error Resume Next
isEqual = N1 Like N2
End Function
‘ Всё очень просто! Теперь проверим N1>N2?:
Public Function isLarger(ByVal N1 As String, ByVal N2 As String) As Boolean
On Error Resume Next
Dim L As Long, I As Long, B1 As Byte, B2 As Byte
L = Len(N1)
If L <> Len(N2) Then
isLarger = L > Len(N2) ‘если длины чисел не равны, то больше то, чья длина больше!
Else
‘ Теперь длины чисел равны…
If N1 Like N2 Then
isLarger = True ‘ проверка случая N1=N2
Exit Function
End If
isLarger = False ‘ теперь: N1<>N2 и у них одинаковая длина -> поразрядная проверка:
For I = 1 To L
B1 = CByte(Mid$(N1, I, 1))
B2 = CByte(Mid$(N2, I, 1))
Select Case B1
Case Is < B2: Exit Function ‘ N1<N2
Case Is > B2 ‘ N2<N1
isLarger = True
Exit Function
End Select
Next
End If
End Function
Public Function LongAdd(ByVal N1 As String, ByVal N2 As String) As String
‘ Самая нужная и полезная функция (также как и вычитание)! Ведь на её основе можно сделать умножение и возведение в степень.
‘ На основе вычитания можно сделать деление и MOD
On Error Resume Next
Dim Tmp As String, Pre As String, Mas() As Byte, L As Long, I As Long
‘ сделаем так, чтобы в N1 хранилось более длинное число, к N2 припишем недостающие разряды нулями.
If Len(N2) > Len(N1) Then
Tmp = N1
N1 = N2
N2 = Tmp
End If
L = Len(N1)
N2 = String$(L - Len(N2), "0") & N2
‘ А вот и массив! Заметьте, что его размер 1..L. Хотя в результате может получиться число длиной максимум L+1
ReDim Mas(1 To L)
‘ Заполняем каждый элемент массива соответствующей суммой
For I = 1 To L
Mas(I) = CByte(Mid$(N1, I, 1)) + CByte(Mid$(N2, I, 1))
Next
‘ Начиная с предпоследней ячейки, нормализуем массив. Число 48 прибавляется, чтобы правильно конвертировать массив в String.
For I = L - 1 To 1 Step -1
If Mas(I + 1) > 9 Then Mas(I) = Mas(I) + 1
Mas(I + 1) = (Mas(I + 1) Mod 10) + 48
Next
‘ Проверяем, не вылез ли L+1 разряд
If Mas(1) > 9 Then
Pre = "1"
Mas(1) = Mas(1) + 38 ‘ 38=48-10
Else
Pre = ""
Mas(1) = Mas(1) + 48
End If
‘ Конвертируем массив в String
Tmp = StrConv(Mas, vbUnicode)
I = InStr(Tmp, Chr(0))
If I > 0 Then Tmp = Left$(Tmp, I - 1)
‘ Опля, всё готово!
LongAdd = Pre & Tmp
End Function
Public Function LongSub(ByVal N1 As String, ByVal N2 As String) As String
‘ действие обратное сложению, не менее полезно. Начало эквивалентно LONGADD:
On Error Resume Next
Dim Tmp As String, Mas() As Byte, L As Long, I As Long
If Len(N2) > Len(N1) Then
Tmp = N1
N1 = N2
N2 = Tmp
End If
L = Len(N1)
N2 = String$(L - Len(N2), "0") & N2
ReDim Mas(1 To L)
For I = 1 To L
Mas(I) = 10 + CByte(Mid$(N1, I, 1)) - CByte(Mid$(N2, I, 1)) ‘ а здесь отнимаем!
Next
For I = L - 1 To 1 Step -1
If Mas(I + 1) < 10 Then Mas(I) = Mas(I) - 1 Else Mas(I) = Mas(I) ‘ и здесь небольшое отличие
Mas(I + 1) = Mas(I + 1) Mod 10
Next
Mas(1) = Mas(1) Mod 10 ‘ проверка на L+1 разряд не нужна.
For I = 1 To L
Mas(I) = Mas(I) + 48 ‘ корректируем значения для StrConv
Next
‘ MAS->String
Tmp = StrConv(Mas, vbUnicode)
I = InStr(Tmp, Chr(0))
If I > 0 Then Tmp = Left$(Tmp, I - 1)
‘ Убираем лишние нули из начала числа
Tmp = ResetZero(Tmp)
‘ Если N1=N2, то мы столкнёмся с этой неприятной ситуацией:
If Tmp = "" Then LongSub = "0" Else LongSub = Tmp
End Function
Теперь будем умножать длинное число на число из диапазона 0..9:
Public Function LongMultOn1Digit(ByVal N1 As String, ByVal N2 As Byte) As String
On Error Resume Next
Dim I As Long, Mas() As Byte, L As Long, Tmp As String
L = Len(N1)
‘ Массив делаем на 1 длиннее, чем число N1 т.к. 33*2=66, но 99*2=198. Последний элемент будет содержать возможный новый разряд.
ReDim Mas(1 To L + 1)
For I = 1 To L
Mas(I + 1) = CByte(Mid$(N1, I, 1)) * N2 ‘ Эквивалентно LongAdd
Next
‘ Нормализуем каждый элемент массива, начиная с предпоследнего (N.B. c L т.к. элементов L+1) и прибавляем 48.
For I = L To 1 Step -1
Mas(I) = Mas(I) + Int(Mas(I + 1) / 10)
Mas(I + 1) = (Mas(I + 1) Mod 10) + 48
Next
Mas(1) = Mas(1) + 48
Tmp = StrConv(Mas, vbUnicode)
I = InStr(Tmp, Chr(0))
If I > 0 Then Tmp = Left$(Tmp, I - 1)
‘ Мы сдвинули массив на 1 вправо, поэтому появление нового разряда мы контролируем в первом символе строки!!!
If Left$(Tmp, 1) = "0" Then Tmp = Right$(Tmp, L)
LongMultOn1Digit = Tmp
End Function
Умножение одного длинного числа на другое (очень трудоёмкая -> самая долго считающая функция)
Public Function LongMult(ByVal N1 As String, ByVal N2 As String) As String
On Error Resume Next
Dim Tmp As String, Mas() As Long, L As Long, I As Long, J As Long, ByteMas() As Byte, P As Long
‘ в начале как всегда!
If Len(N2) > Len(N1) Then
Tmp = N1
N1 = N2
N2 = Tmp
End If
L = Len(N1)
N2 = String$(L - Len(N2), "0") & N2
‘ Массив берём из 2*L элементов. Т.к. 99*99=9801
ReDim Mas(1 To 2 * L)
For I = 1 To L * 2
Mas(I) = 0
Next
For I = L To 1 Step -1
For J = L To 1 Step -1 ‘ двойной цикл… вот тут-то и влияние на скорость!
P = I + J ‘ адрес куда будем класть результат. Вспоминайте перемножение столбиком!
Mas(P) = Mas(P) + CLng(Mid$(N1, J, 1)) * CLng(Mid$(N2, I, 1))
Next
Next
‘знакомая нам нормализация массива начинаемая с предпоследнего элемента
P = 2 * L - 1
For I = P To 1 Step -1
J = I + 1
Mas(I) = Mas(I) + Int(Mas(J) / 10)
Mas(J) = (Mas(J) Mod 10) + 48
Next
Mas(1) = Mas(1) + 48
‘теперь Long mas -> byte mas (для того, чтобы можно было использовать StrConv)
ReDim ByteMas(1 To 2 * L)
P = 2 * L
For I = 1 To P
ByteMas(I) = CByte(Mas(I))
Next
‘ тоже как всегда...
Tmp = StrConv(ByteMas, vbUnicode)
I = InStr(Tmp, Chr(0))
If I > 0 Then Tmp = Left$(Tmp, I - 1)
LongMult = ResetZero(Tmp) ‘и последний штрих: удаляем лишние нули. А их может быть очень много
End Function
А вот и самая сложная из операций (по моему опыту). LongDiv писалась основываясь на LongMod. Чтобы лучше понять смысл, внимательно разберите приводимый выше пример.
Public Function LongMod(ByVal N1 As String, ByVal N2 As String) As String
On Error Resume Next
Dim I As Long, Tmp As String, Mas(1 To 9) As String
LongMod = "0"
‘ Напомню:
‘ a mod a=0
‘ a mod 1=0
‘ поэтому:
If Not ((N2 = "1") Or (N1 Like N2)) Then
‘ будем действовать пока N1>N2. Ведь иначе mod=n1 или 0!!!
Do While isLarger(N1, N2)
‘ N2<N1 -> в Tmp мы шлём N2 предварительно уравнивая его с N1 по длине (нули дописываем в конец числа, тем самым как бы умножая его на 10 в нужной степени).
Tmp = N2 & String$(Len(N1) - Len(N2), "0")
If Tmp Like N1 Then Exit Function ‘ Tmp=N1?
If isLarger(Tmp, N1) Then Tmp = Left$(Tmp, Len(Tmp) - 1) ‘ если с нулями переборщили, то один придётся убрать
‘ заполняем массив числами Tmp, Tmp*2, Tmp*3,... до нужных пор
Mas(1) = Tmp
For I = 2 To 10
Mas(I) = LongAdd(Mas(I - 1), Tmp)
If isLarger(Mas(I), N1) Or (Mas(I) Like N1) Then Exit For
Next
N1 = LongSub(N1, Mas(I - 1)) ‘ уменьшаем N1 на последнее из полученных значений
Loop
LongMod = N1 ‘ петля закончилась, вот Вам и модуль!
End If
End Function
‘ Деление нацело полностью основано на LongMod! Функция возвращает целую часть, остаток передаётся через параметр Ostatok
Public Function LongDiv(ByVal N1 As String, ByVal N2 As String, ByRef Ostatok As String) As String
On Error Resume Next
Dim I As Long, Tmp As String, Mas(1 To 9) As String, IntPart As String, PreIntPart As String
LongDiv = "0"
Ostatok = "0"
‘ В начале некоторые частные случаи деления:
If N1 = "0" Then Exit Function
If N2 = "0" Then
MsgBox "ERROR: Division by Zero!"
Exit Function
End If
If N2 = "1" Then
LongDiv = N1
Ostatok = "0"
Exit Function
End If
If N1 Like N2 Then
LongDiv = "1"
Exit Function
End If
If isLarger(N2, N1) Then
Ostatok = N1
Exit Function
End If
‘ А дальше несколько дополненный LongMod. Пусть разбор этого примера будет на Вашей совести
IntPart = "0"
Ostatok = N1
Do While isLarger(Ostatok, N2)
Tmp = N2 & String$(Len(Ostatok) - Len(N2), "0")
PreIntPart = "1" & String$(Len(Ostatok) - Len(N2), "0")
If Tmp Like Ostatok Then
LongDiv = LongAdd(IntPart, PreIntPart)
Ostatok = "0"
Exit Function
End If
If isLarger(Tmp, Ostatok) Then
Tmp = Left$(Tmp, Len(Tmp) - 1)
PreIntPart = Left$(PreIntPart, Len(PreIntPart) - 1)
End If
Mas(1) = Tmp
For I = 2 To 10
Mas(I) = LongAdd(Mas(I - 1), Tmp)
If isLarger(Mas(I), Ostatok) Or (Mas(I) Like Ostatok) Then Exit For
Next
IntPart = LongAdd(IntPart, Replace$(PreIntPart, "1", I - 1))
Ostatok = LongSub(Ostatok, Mas(I - 1))
Loop
LongDiv = IntPart
End Function
Public Function LongPower(ByVal N1 As String, ByVal N2 As Long) As String
‘ Выполняем операцию N1^N2 рекурсивно. Глубина рекурсии: int(Ln(N2)/Ln(2))
On Error Resume Next
Select Case N2
Case 0: LongPower = "1" ‘ 2 точки выхода из рекурсии
Case 1: LongPower = N1
Case Else
Dim Ret As String
Ret = LongPower(N1, Int(N2 / 2)) ‘ делим степень нацело на 2 и опять в рекурсию…
‘ если степень чётна, то при выходе из рекурсии (здесь идёт уже обратный ход!!!) достаточно перемножить полученные на предыдущем шаге рекурсии результаты, в случае нечётности степени, надо ещё дополнительно умножить на основание!
If N2 Mod 2 = 0 Then LongPower = LongMult(Ret, Ret) Else LongPower = LongMult(LongMult(Ret, Ret), N1)
End Select
End Function
Дополнительная
информация:
По
поводу усовершенствования алгоритмов, найденных ошибок, комментариев: yxine@mail.ru
Сайт
автора: http://yxine.km.ru
Скачать
статью в Doc: http://yxine.km.ru/download.asp?s=longmathdoc